Садреев И.Р., Фирсов Ю.В.

«Нефтяное хозяйство», 2000, №1

САМОТЕЧНОЕ ДВИЖЕНИЕ НЕФТИ ПРИ ПОРЫВЕ И ОСТАНОВКЕ ТРУБОПРОВОДА

 

Представлен метод расчета самотечного движения жидкости по отсеченному с двух сторон герметичными задвижками участку трубопровода, проложенному по реальному рельефу местности, при сливе жидкости из трубопровода через сливное отверстие (утечку). Проведены расчеты остановки конкретного нефтепровода и выполнено сравнение полученных результатов с экспериментальными данными.

 

            В системах магистральных нефтепроводов существуют режимы работы, когда движение нефти можно считать безнапорным. Как правило, таким течениям предшествует напорное движение нефти. Истечение нефти при порывах и остановках нефтепроводов как раз относятся к подобному классу течений, а именно напорное движение нефти сменяется самотечным.

            Исследование таких течений является чрезвычайно важными для безопасной и эффективной эксплуатации системы трубопроводного транспорта нефти и нефтепродуктов. Анализ сброса нефти при порывах позволяет в зависимости от режима работы и свойств нефти оптимизировать циклограмму останова нефтепроводов с точки зрения минимального розлива нефти для любого места и интенсивности порыва, а также оперативно определять количество вытекшего продукта при аварии. Аналогичная расчетная задача возникает при определении полного объема и динамики слива нефти при раскачке участка нефтепровода с целью ремонта трубы или замены технологического оборудования на отсеченном участке, а также при остановке нефтепровода со значительной задержкой закрытия задвижек после отключения насосов.

            Весь процесс истечения нефти при порыве по времени можно разделить на четыре стадии (течение нефти при остановке нефтепровода с задержкой в закрытии приемной или выкидной задвижки при подходящем рельефе местности проходит те же стадии):

            1) выплескивание части жидкости из места разрыва в процессе перекачки, т.е. до момента выключения насосов и перекрытия задвижек;

            2) нестационарные процессы в трубопроводе, вызванные остановкой насосов и перекрытием задвижек;

            3) истечение жидкости из отсеченного участка трубопровода под действием начального сжатия (продолжается до момента падения давления до точки кипения в какой-либо точке трубопровода);

            4) истечение жидкости из части отсеченного участка под действием силы тяжести и давления насыщенного пара.

            Для описания движения нефти на первых трех стадиях можно пользоваться хорошо разработанным математическим аппаратом метода характеристик в рамках механики сплошной среды. Четвертая стадия представляет собой самотечное движение нефти в трубопроводе, математический аппарат для описания такого движения в настоящее время разработан недостаточно. Следует отметить, что с точки зрения протекания физического процесса, а следовательно и математических методов решения, такое деление на стадии по времени является весьма условным. Например, из-за значительной протяженности нефтепровода и сжимаемости среды, т.е. конечности скорости звука (c»1000м/с), в некоторых местах давление может упасть до давления насыщенных паров, иными словами произойти разрыв сплошности потока, в то время как в других - нефть останется под давлением начального сжатия. Поскольку в один и тот же момент времени нельзя часть трубопровода описывать одной моделью, а часть другой, стыковка решений, полученных методом характеристик в рамках механики сплошной среды и при самотечном течении, также требует специального рассмотрения.

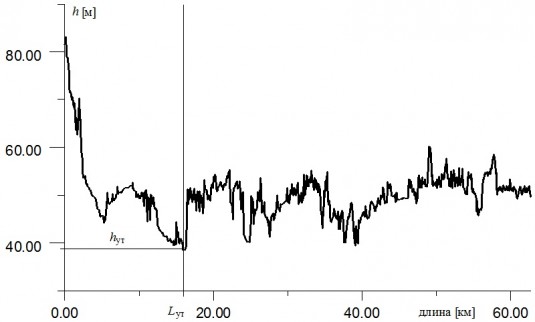
            В качестве примера рассмотрим нефтепровод, трассовка которого представлена на рис.1. Разобьем всю трассу на последовательность ориентированных в пространстве и состыкованных между собой цилиндров. Каждый цилиндр будет характеризоваться отметками высот верхней образующей в крайних точках, диаметром и протяженностью (длиной участка). Для каждого цилиндра определим горизонтальную плоскость, выше которой нефть может вытечь через порыв. Для этого значения высот верхних образующих в крайних точках рассматриваемого цилиндра сравним с абсолютной вакууметрической высотой h=h_ут+(P_а-P_s)/rg(P_а - атмосферное давление, P_s - давление насыщенных паров нефти) относительно высоты места утечки и со значением нижней образующей наивысшей точки трассы, расположенной между рассматриваемым цилиндром и местом  утечки. После чего для каждого цилиндра вычислим объем V_i, лежащий выше этой плоскости. Далее объемы нефти, слившейся с отдельных цилиндров, просуммируем. Это и будет тот объем, который может вытечь с отсеченного участка нефтепровода через порыв (далее будем считать, что участок отсечен в крайних точках трассы).

 

 

Рис. 1. Профиль нефтепровода

 

            Зная для каждого цилиндра геометрическую форму той части объема, которая может вытечь, найдем координаты центра тяжести этих объемов. Пусть для цилиндров, расположенных справа от места утечки, этими координатами будут h_ir,L_ir (i=1....I, L_ir-L_ут>L_i+1,r-L_ут) и в них располагаются объемы жидкости V_ir, а слева объемы V_jl имеют координаты h_jl,L_jl (j=1....J, L_ут-L_jl>L_ут-L_j+1,l). Здесь и далее, все, что находится справа от утечки, имеет индекс - r, а слева - l.Таким образом от динамической задачи самотечного слива с распределенными параметрами по нефтепроводу мы перешли к задаче с дискретными значениями.

            Предположим вначале, что слив происходит только с левой части нефтепровода, а h_1l>h_jl (j>1), т.е. самый удаленный объем, который может вытечь, имеет наибольшую высоту. Уравнение, описывающее движение нефти по нефтепроводу из точки с координатами h_1l,L_1l через порыв, запишем в виде

 

f(Q)×(L_ут-L_1l)+x_u×Q²-rg(h_1l-h_ут)+P_а-P_s=0                                                                               (1)

где   2x_u=r/(mF_u)²  - коэффициент сопротивления отверстия слива,

         m-коэффициент   расхода через отверстие,

         F_u -площадь отверстия слива,

         Q - объемный расход по нефтепроводу,

         f(Q)=С×Q^1.75, C=0.24rn^0.25/D^4.75 - сопротивление трубы по Блазиусу, D - диаметр

                   трубопровода, n- вязкость нефти.

            При этом давления в промежуточной точке с координатами (h_jl,L_jl)  будет равно:

 

P_jl(h_jl,L_jl)=P_s-f(Q_1l)×(L_jl-L_1l)+rg(h_1l-h_jl)                                                                                 (2)

 

здесь Q_1l - решение уравнения (1).

            Из формулы (2) видно, что возможна ситуация, когда давление в рассматриваемой точке будет меньше давления насыщенных паров жидкости P_s. Чтобы этого не случилось, необходимо уменьшить расход на участке между точками с координатами h_1l,L_1l и h_jl,L_jl.  Пусть ближайшей к точке с индексом - 1 будет точка с индексом - k, где давление упало ниже P_s, тогда новое значение Q_1l^* в соответствии с формулой (2) найдем из уравнения

 

f(Q_1l^*)×(L_kl-L_1l)-rg(h_1l-h_kl)=0                                                                                                 (3)

 

            На участке между точкой с координатами h_kl,L_kl и местом утечки расход должен скачком увеличиться, а значение его можно найти из уравнения аналогичное уравнению (1), а именно

 

f(Q_1l^*+Q_kl)×(L_ут-L_kl)+x_u×(Q_1l^*+Q_kl)²-rg(h_kl-h_ут)+P_а-P_s=0                                                      (4)

 

Здесь Q_kl - расход с которым опорожняется объем V_kl, находящийся в точке с координатами h_kl,L_kl. В соответствии с вышеописанной процедурой, двигаясь дальше к месту утечки, можно найти расходы с которыми опорожняются все объемы, расположенные по левую сторону от места слива, а следовательно, и время опорожнения каждого объема t_jl=V_jl/Q_jl. Пусть t_min=t_ml, т.е. первым стечет объем с индексом - m. Тогда через время t=t_minобъем с индексом - m исчезнет, а значения остальных объемов V_jl, из которых происходит слив, уменьшатся на величину t_min×Q_jl. На следующим шаге объем с индексом - m исключим из рассмотрения, а всю выше описанную процедуру проделаем для оставшихся L-1 объемов.

            В случае двустороннего слива на каждом расчетном шаге сначала отдельно решим задачу для слива с правой части (т.е. как бы участка нефтепровода слева от места утечки не существует) и с левой части. Далее найдем совместное решение для слива с двух сторон. Для этого рассмотрим наиболее близкие справа и слева от места утечки точки из которых происходит односторонний слив. Пусть это будут точки с координатами L_Ir,h_Ir и L_Jl,h_Jl. Решая систему уравнений

 

 

f(Q_r)×(L_Ir-L_ут)+x_u×(Q_r+Q_l)²-rg(h_Ir-h_ут)+P_а-P_s=0

                                                                                                                                              (5)

f(Q_l)×(L_ут-L_Jl)+x_u×(Q_r+Q_l)²-rg(h_Jl-h_ут)+P_а-P_s=0,

 

найдем новые значения расходов справа и слева через порыв. Не трудно показать, что новые расходы с каждой стороны будут не больше, чем при одностороннем сливе, а суммарный расход не меньше, чем любой из расходов при одностороннем сливе. Из этого следует, что в следующей по удалению справа и/или слева от места порыва точке из которой происходит слив, давление может подняться больше давления насыщенных паров. В этом случае систему уравнений (5) надо решать не для точек с координатами L_Ir,h_Ir и L_Jl,h_Jl, а для следующих по удалению от места порыва точек, где давление поднялось выше P_s. Такая операция выполняется до тех пор, пока давление во всех оставшихся точках не будет равно P_s. Следует отметить, что при таком расчете возможно появление двух комбинаций точек справа и слева (т.е. двух решений), причем в обеих комбинациях во всех точках с которых происходит слив выполняется условие P=P_s. В этом случае выбирается то решение, при котором больше суммарный расход через порыв. При таком выборе обеспечивается монотонное уменьшение суммарного расхода через порыв по времени, что соответствует общефизическим представлениям о самотечном сливе.

            На основе предложенной модели течения на C++ была составлена расчетная часть программы самотечного слива с однониточного трубопровода. В плане интерфейса разработаны две принципиально различные программы: одна работает под DOS, другая - под Windows 95.

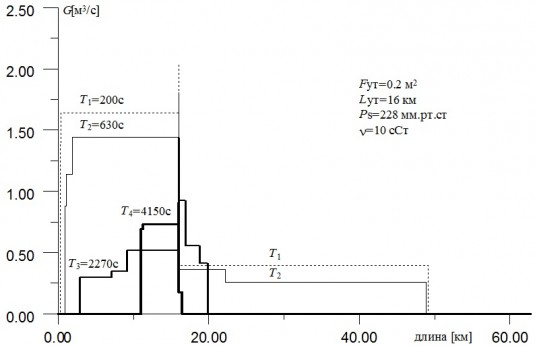
            В качестве примера рассмотрим нефтепровод (D»1.2м), трассовка которого представлена на рис.1. На рис.2 представлены распределения объемного расхода по длине нефтепровода, отсеченного герметичными задвижками в крайних точках трассы, в различные моменты времени при утечке нефти через порыв площадью 0.2м² (см. рис.1). Видно, что нефть может стекать одновременно из нескольких точек, например, в момент времени T=T₃ нефть стекает одновременно справа из трех точек и слева из трех точек.

 

 

Рис.2 Распределение расхода по длине в разные моменты времени

 

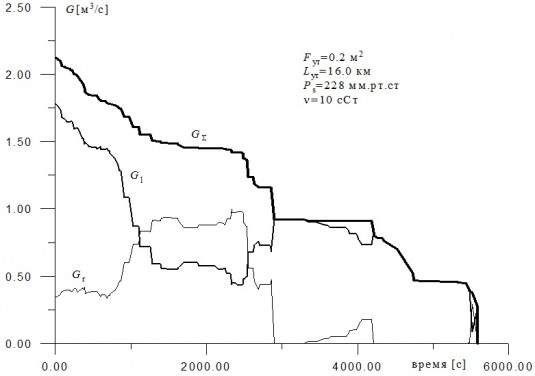
            Графики на рис.3 представляют собой зависимости суммарного объемного расхода - G_Sот времени через порыв, а также отдельно расходов с правой - G_r и с левой - G_l стороны от места порыва. Видно, что суммарный расход монотонно убывает с течением времени. Кроме того в отдельные моменты времени расход справа может превышать расход слева, а в некоторые - наоборот. Приблизительно через 1.5часа самотечный слив через порыв прекращается. Проинтегрировав зависимость G_Sпо времени, получим суммарный объем вытекшей через порыв нефти. Эта величина для данного случая оказалась равной 6459.2м³.

 

 

Рис.3 Зависимость расхода справа, слева и суммарного расхода от времени

 

            Стыковку решений, полученных методом характеристик и в рамках представленной модели самотечного слива, рассмотрим на примере останова нефтепровода, упрощенная схема которого изображена на рис.4 и выглядит следующим образом (трассовка между задвижками №1 и №2 показана на рис.1)

 

Рис.4 Расчетная схема нефтепровода

 

В эксперименте на стационарном режиме один подпорный насос обеспечивал перекачку 9100т/2ч при избыточном давлении на выкиде насосной станции »0.6МПа. После остановки насоса выкидная задвижка (на схеме задв. №1) закрывалась 135с. Задвижка на приеме вообще не закрывалась вплоть до прекращения течения на приеме в РП. Уровень нефти в приемном РП был равен 7.9м. Между приемной задвижкой №2 и РП был установлен ультразвуковой расходомер (УЗР) типа PT868 фирмы PANAMETRICS, который обеспечивал измерение мгновенного расхода.

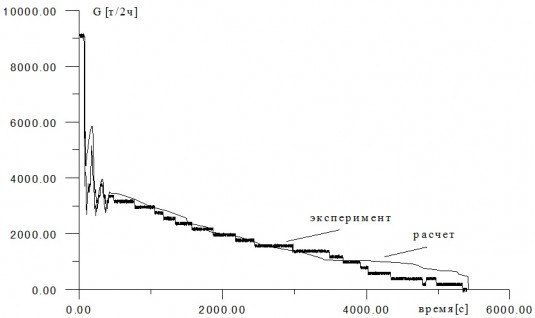
            На рис.5 представлен мгновенный расход нефти на приеме в РП при остановке нефтепровода, определенный экспериментальным и расчетным путем. До момента закрытия задвижки №1 расчет проводился методом характеристик, далее в течении времени 3.5L/c (L - длина нефтепровода, c - скорость звука в нефтепроводе, в условиях проведения эксперимента с=930м/c) расчет также проводился методом характеристик, но с зависящей от времени весовой функцией при определении значения расхода на приеме, обеспечивающей непрерывность величины расхода при переходе от расчета методом характеристик к модели самотечного течения. Далее расчет проводился по вышеописанной модели безнапорного течения. Вязкость нефти в программе расчета определялась по параметрам стационарного режима (потери давления в нефтепроводе расчитывались по Блазиусу).

 

 

Рис.5 Зависимость расхода нефти от времени на приеме в РП при остановке нефтепровода без закрытия приемной задвижки

 

            Видно, что имеет место хорошее не только качественное, но и количественное совпадение экспериментальных и расчетных данных, как в интервале времени, когда расчет проводился методом характеристик, так и в интервале времени, когда расчет проводился по модели безнапорного течения. Следует отметить, что время между моментом перекрытия рассматриваемого участка задвижками и моментом перехода в расчетах к модели самотечного слива, равное в приведенном примере 3.5L/c,в каждом конкретном случае исходя из физических соображений может меняться, а его величина требует специального подбора.

            Вывод.С учетом разрыва сплошности среды разработан метод расчета безнапорного движения жидкости по нефтепроводам. Исследован вопрос стыковки полученного решения с решением в рамках модели течения сплошной среды. Проведенное сравнение показало хорошее совпадение расчетных и экспериментальных данных.

 

 Садреев Ильдар Римович

г. Нижневартовск, Нижневартовское УМН АО «Сибнефтепровод», 

 

Фирсов Юрий Владимирович

г. Москва, ООО «Энергоавтоматика»